Pugh's closing lemma

In mathematics, Pugh's closing lemma is a result that links periodic orbit solutions of differential equations to chaotic behaviour. It can be formally stated as follows:

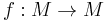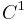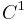Let $f:M \to M$ be a $C^1$ diffeomorphism of a compact smooth manifold $M$ . Given a nonwandering point $x$ of $f$ , there exists a diffeomorphism $g$ arbitrarily close to $f$ in the $C^1$ topology of 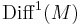$\operatorname{Diff}^1(M)$ such that $x$ is a periodic point of $g$ .^[1]

Interpretation

Pugh's closing lemma means, for example, that any chaotic set in a bounded continuous dynamical system corresponds to a periodic orbit in a different but closely related dynamical system. As such, an open set of conditions on a bounded continuous dynamical system that rules out periodic behaviour also implies that the system cannot behave chaotically; this is the basis of some autonomous convergence theorems.

References

^ Pugh, Charles C. (1967). "An Improved Closing Lemma and a General Density Theorem". American Journal of Mathematics 89 (4): 1010–1021. doi:10.2307/2373414.

This article incorporates material from Pugh's closing lemma on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Pugh's closing lemma

Interpretation

See also

References